Chapter 8. Space Curves

Rovenski Vladimir, Haifa

> restart:

8.1 Introduction

8.1.1 Commands spacecurve and tubeplot

1. The curve lies in a plane.

> r1:=[1, 2, 1]: r2:=[3, -2, 0]: r3:=[2, -4, -1]: linalg[det]([r1, r2, r3]);

> with(plots):

Warning, the name changecoords has been redefined

> A:=spacecurve(evalm(r1+t*r2+t^2*r3), t=-2..2, thickness=3, color=red): B:=plot3d(evalm(u*r1+v*r2), u=-4..2, v=-1..7): display([A,B], orientation=[30,70], axes=boxed);

2. Using cycloidal curves we obtain three-dimensional curves: astroid (m= -1/4), deltoid (m= -1/3),

nephroid (m= 1/2), cardioid (m= 1), three-dimensional roses, etc.

> m:=-1/4: h:=1: # 3-dimensional astroid, then enter your data

> r3:=[(1+m)*cos(m*t)-h*m*cos(t+m*t), (1+m)*sin(m*t)-h*m*sin(t+m*t), cos(t)]:

> plots[spacecurve](r3, t=0..2*Pi/abs(m), axes=boxed,thickness=2);

3. Two engaged circles (tori).

> plots[tubeplot]({[cos(t), sin(t), 0], [0, cos(t)+.8, sin(t)]}, t=0..2*Pi, radius=.25, tubepoints=40, orientation=[0,60], lightmodel=light2, style=patchnogrid);

>

A chain containing 2n circles.

> n:=3: P:=i->plots[tubeplot]({[2*cos(t),2*sin(t)+6*i,0], [0,2*cos(t)+3+6*i,2*sin(t)]}, t=0..2*Pi, radius=.4, orientation=[0,60], style=patchnogrid, lightmodel=light4):

> plots[display]([seq(P(i),i=0..n-1)], scaling=constrained);

The chain armor with m lines.

> n:=4: m:=4: P:=(i,j)->tubeplot({[2*cos(t)+6*j, 2*sin(t)+6*i,0], [6*j,2*cos(t)+3+6*i, 2*sin(t)], [2*cos(t)-3+6*i, 0+6*j,2*sin(t)]}, t=0..2*Pi, radius=.4, orientation=[40,50], style=patchnogrid, lightmodel=light4): display([(seq(seq(P(i,j), i=0..n), j=0..m))], scaling=constrained);

8.1.2. Intuitive Projection

A part of the hyperboloid of one sheet (two methods).

> m:=11: n:=50: T:=i->i*2*m*Pi/n: # First method

> p1:=plot([seq([cos(T(i)), .5*sin(T(i))+(-1)^i], i=1..m*n)]): p2:=plot([[cos(t), 0.5*sin(t)+1, t=0..2*Pi], [cos(t), 0.5*sin(t)-1, t=0..2*Pi]]): plots[display]([p1, p2], scaling=constrained);

> m:=8: n:=3*m: T:=i-> i*2*Pi/n: # second method

> p1:=plot([seq([[cos(T(i)), 0.5*sin(T(i))-1], [cos(T(i+m)), 0.5*sin(T(i+m))+1]], i=1..n)]): p2:=plot([[cos(t), .5*sin(t)+1, t=0..2*Pi], [cos(t), .5*sin(t)-1, t=0..2*Pi]]): plots[display]([p1, p2], scaling=constrained);

>

8.2. Knitting on Surfaces of Revolution

8.2.1. Simplified Model of Projection

Example 1 . Isometric and dimetric projections of a helix on the catenoid.

> with(plots):

> t1:=4: isoaxes:=polygonplot([[[0,0], [-t1,-t1/2]], [[0,0], [t1,-t1/2]], [[0,0], [0,t1]]]): #isometric

> f:=cosh(t): g:=4*t: # enter your data

> a:=20: X:=f*cos(a*t): Y:=f*sin(a*t): Z:=g:

> isom:=plot([Y-X, Z-(X+Y)/2, t=-3..3]):

> display([isom, isoaxes], axes=none, scaling=constrained);

> t1:=4: diaxes:=polygonplot([[[0,0], [-t1/2,-t1/2]], [[0,0], [t1,0]], [[0,0], [0,t1]]]): # dimetric

> f:=cosh(t): g:=4*t: # enter your curve

> a:=20: X:=f*cos(a*t): Y:=f*sin(a*t): Z:=g:

> dimetr:=plot([Y-X/2, Z-X/2, t=-3..3]):

> display([dimetr, diaxes], axes=none, scaling=constrained);

>

8.2.2. Main Model of Projection

Example 1 . Plot the space curves lying on a cylinder and a cone:

1. The circular helix .

A generalization is a curve r(t)= [a cos t, b sin t, ct] on an elliptic cylinder.

> R:=1: a:=1: spacecurve([R, t, a*t, t=0..16*Pi], coords=cylindrical, numpoints=250, orientation=[40,70]);

2.

(a) 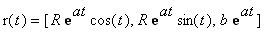, a conic helix.

> a:=.05: spacecurve([exp(a*t), t, exp(a*t), t=0..16*Pi], coords=cylindrical, numpoints=150, orientation=[40,70], axes=boxed);

(b) , circular conic helix.

> a:=.05: spacecurve([a*t, t, t, t=-14*Pi..14*Pi],coords=cylindrical, numpoints=350, orientation=[40,70], axes=boxed);

Example 2 . Springs on surfaces of revolution (see Section 20.2).

1. The curve lies on the paraboloid of revolution,

and projecs onto the plane XY as Archimedes' spiral.

> a:=1: spacecurve([a*t, t, t^2/2, t=0..24*Pi], coords=cylindrical, numpoints=500, orientation=[40,73], axes=boxed);

2. The curve lies on a hyperboloid of revolution.

> a:=.06: spacecurve([cosh(a*t), t, sinh(a*t), t=-12*Pi..12*Pi], coords=cylindrical, numpoints=300, orientation=[40,73], axes=boxed);

3. The curve (c) lies on an ellipsoid (on a sphere if a=b=c.)

> R:=1: a:=28: spacecurve([R, a*t, t, t=0..Pi], coords=spherical, numpoints=300, orientation=[20, 76], axes=boxed);

4. Several complicated curves on a sphere.

> m:=7: n:=10: X:=cos(m*t)*cos(n*t): Y:=sin(m*t)*cos(n*t): Z:=sin(n*t):

> plots[tubeplot]([X,Y,Z, radius=.05], t=-Pi..Pi, color=[1,.8,.1], ambientlight=[.4,.4,.4], light=[75,50,1,.9,.5], orientation=[0,26], numpoints=450, scaling=constrained);

For m:=1: n:=17: and t=-Pi/2..Pi/2 we obtain the curve consisting of 17 meridians.

5. For the torus knot K{8,27} we assume and .

> m:=27: n:=8: X:=(3+cos(m*t))*cos(n*t): Y:=(3+cos(m*t))*sin(n*t): Z:=sin(m*t):

> plots[tubeplot]([X,Y,Z, radius=.1], t=-Pi..Pi, color=[1,.8,.1], ambientlight=[.4,.4,.4], light=[75,50,1,.9,.5], orientation=[0, 60], numpoints=450, scaling=constrained);

>

8.3. Plotting of Curves (Tubes) with Shadow

Example 1 .

(a) The parallel projections of the circular helix onto the plane orthogonal to its axis

are the usual curtate or prolate cycloids. In next program, helix denotes the circular helix (tube);

T denotes vertices and faces of the tray (parallelepiped);

Tray denotes the image of the tray; {shadow} denotes the shadow of the curve.

> with(plots):

> A:=0: B:=0: C:=1: lv:=75: lh:=38: oh:=12: ov:=60:

> a:=evalf(sin((lv-(90-ov))/180*Pi)*cos((lh+oh)/180*Pi)): b:=evalf(sin((lv-(90-ov))/180*Pi)*sin((lh+oh)/180*Pi)): c:=evalf(cos((lv-(90-ov))/180*Pi)):

> R:=5: V:=.8: X:=R*cos(t): Y:=R*sin(t): Z:=V*t:

> helix:=tubeplot([X, Y, Z, radius=0.5], t=0..7*Pi, numpoints=90, tubepoints=20, ambientlight=[.5, .5, .5], light=[lv, lh, .6, .8, .2]):

> Xs:=((b*B+c*C)*X-a*B*Y-a*C*Z)/(a*A+b*B+c*C): Ys:=(-b*A*X+(a*A+c*C)*Y-b*C*Z)/(a*A+b*B+c*C): Zs:=(-c*A*X-c*B*Y+(a*A+b*B)*Z)/(a*A+b*B+c*C):

> shadow:=tubeplot([Xs,Ys,Zs, radius=.5], t=0..7*Pi, numpoints=70, tubepoints=20, color=[.2,.3,.5]):

> T:=[[[8,-22,-.01], [-18,-22,-.01], [-18,8,-.01],[8,8,-.01]], [[8,-22,-1], [8,8,-1], [-18,8,-1],[-17,-22,-1]], [[8,8,-.01], [8,-22,-.01], [8,-22,-1],[8,8,-1]], [[8,8,-1], [8,8,-.01], [-18,8,-.01],[-18,8,-1]], [[-18,8,-.01], [-18,8,-1], [-18,-22,-1],[-18,-22,-.01]], [[-18,-22,-.01], [-18,-22,-1],[8,-22,-1], [8,-22,-.01]]]:

> tray:=polygonplot3d(T, color=COLOR(RGB, .4, .7, .2)):

> display3d([helix, shadow, tray], orientation=[oh,ov]);

>

(b) The central projection of the circular helix onto the plane orthogonal to its axis

from a point on the helix is the cochleoid

In the next program, the center of projection lies at the height {h}; helix denotes the circular helix (tube);

T denotes vertices and faces of the tray (parallelepiped); Tray denotes the image of the tray; shad1 denotes

the shadow of the part of the curve below the center of projection; {shad2} denotes the shadow of the part of

the curve over the center.

> with(plots):

> lv:=75: lh:=38: oh:=12: ov:=60:

> R:=.8: X:=R*(cos(t)-1): Y:=R*(sin(t)): Z:=.2*t: h:=.2*Pi*8:

> helix:=tubeplot([X, Y, Z, radius=0.3], t=0..16*Pi, numpoints=90, tubepoints=15, ambientlight=[.5, .5, .5], light=[lv, lh, .6, .8, .2]):

> Xs:=h/(h-Z)*X: Ys:=h/(h-Z)*Y: Zs:=0:

> shad1:=tubeplot([Xs, Ys, Zs, radius=.3], t=0..7.95*Pi, numpoints=70, color=[.2, .3, .5]):

> shad2:=tubeplot([Xs,Ys,Zs, radius=.3], t=8.05*Pi..16*Pi, numpoints=70, color=[.2, .3, .5]):

> T:=[[[16,-22,-.01], [-18,-22,-.01], [-18,8,-.01],[16,8,-.01]], [[16,-22,-1], [16,8,-1], [-18,8,-1],[-18,-22,-1]], [[16,8,-.01], [16,-22,-.01], [16,-22,-1],[16,8,-1]], [[16,8,-1], [16,8,-.01], [-18,8,-.01],[-18,8,-1]], [[-18,8,-.01], [-18,8,-1],[-18,-22,-1], [-18,-22,-.01]], [[-18,-22,-.01],[-18,-22,-1], [16,-22,-1], [16,-22,-.01]]]:

> tray:=polygonplot3d(T, color=COLOR(RGB, .4, .7, .2)):

> display3d([helix, shad1, shad2, tray], orientation=[oh,ov]);

>

Example 2 .

For various impressions we plot projections of the (circular helix) curve onto the simple surfaces

(a) cylinder and (b) sphere.

Hints .

(a) Cylinder. We suppose that centers of projection lie on the axis of the cylinder.

In next program, helix denotes the circular helix (tube); cyl denotes the cylinder (frame) with the section;

Tray denotes the surface of the tray (rectangular); shad denotes the shadow of the curve onto the cylinder.

> with(plots):

> cyl:=plot3d([1, x, y], x=-Pi/4..5*Pi/4, y=0..2.5, coords=cylindrical, style=wireframe):

> R:=.2: X:=R*cos(t)+1*8*R: Y:=R*sin(t): Z:=R*t/2:

> helix:=tubeplot([X,Y,Z, radius=R*.6], t=0..6*Pi, numpoints=99, light=[75,40,.8,.7,.3], ambientlight=[.6,.6,.6]):

> Xp:=X/sqrt(X^2+Y^2): Yp:=Y/sqrt(X^2+Y^2): Zp:=Z:

> shad:=tubeplot([Xp,Yp,Zp, radius=R*.6/sqrt(X^2+Y^2)], t=0..6*Pi, numpoints=99, color=[.5,.2,.2]):

> tray:=polygonplot3d([[-2,-2,0], [-2,2,0], [2.5,2,0], [2.5,-2,0]],color=COLOR(RGB,.4,.7,.2)):

> display3d([shad, cyl, helix, tray], orientation=[60,70]);

>

(b) Sphere.

We suppose that the center of the sphere is the center of projection.

In the next program, helix denotes the circular helix (tube); sphere denotes the sphere (frame);

Tray denotes the tray (rectangular); {shad} denotes the shadow of the curve on the cylinder.

> with(plots):

> sphere:=plot3d([1, x, y], x=-Pi/2..Pi/2, y=-Pi/2..3*Pi/2, coords=spherical, style=wireframe):

> R:=.2: X:=R*cos(t)+1*8*R: Y:=R*sin(t): Z:=R*t/2:

> helix:=tubeplot([X, Y, Z, radius=R*.5], t=-2/R..6*Pi, numpoints=99, light=[75,40,.8,.7,.3], ambientlight=[.5,.5,.5]):

> M:=sqrt(X^2+Y^2+Z^2): Xp:=X/M: Yp:=Y/M: Zp:=Z/M:

> shad:=tubeplot([Xp,Yp,Zp, radius=R*.5/M], t=-2/R..6*Pi, numpoints=99, color=[.5,.2,.2]):

> tray:=polygonplot3d([[-2,-2,-1], [-2,2,-1], [2,2,-1], [2,-2,-1]], color=COLOR(RGB, .4, .7, .2)):

> display3d([shad, sphere, helix, tray], orientation=[60,60]);

>

Example 3 .

(a) The curve bicylinder , which for R = r consists of two closed curves, and for R=r breaks up into

two intersecting ellipses, which lie in the planes x= y and x= -y.

In the next program we plot the family of the bicylinders under a change of the radius of one of cylinders.

> with(plots):

> R:=2: m:=6: a:=array(1..m): b:=array(1..m):

> c:=plot3d([R, u, v], u=0..2*Pi, v=-2.5..2.5, coords=cylindrical, style=wireframe):

> for i from 1 to m do r:=R*((2*m+i)/(3*m)): a[i]:=spacecurve([R, t, sqrt(R^2-r^2*sin(t)^2),t=0..2*Pi], coords=cylindrical): b[i]:=spacecurve([R, t, -sqrt(R^2-r^2*sin(t)^2),t=0..2*Pi], coords=cylindrical) od:

> display(c,seq([a[i], b[i]], i=1..m), orientation=[30,80]);

>

(b) The curve of Viviani .

> f:=[cos(t)^2, cos(t)*sin(t), sin(t)]: V:=array(1..2, 0..1):

> for i from 1 to 2 do for j from 0 to 1 do V[i,j]:=spacecurve(f, t=0..2*Pi, orientation=[90*j, 90*i],thickness=3) od od:

> plots[display](V);

>

(c) The sphere of radius R (with the center O) intersects the ellipsoid with the axes a>b>c with the center O.

In the next program we plot the curve (solution of Euler's equations with Y(0)=0) with

the correspondingly intersecting sphere and ellipsoid.

> restart: J_1:=1: J_2:=2: J_3:=16: L:=2.1: E:=1.1: # enter your data

> L^2-2*E*J_2; # check that the expression >0

> omega_01:=sqrt((2*E*J_3-L^2)/(J_1*(J_3-J_1))): omega_02:=sqrt((2*E*J_3-L^2)/(J_2*(J_3-J_2))): omega_03:=sqrt((-2*E*J_1+L^2)/(J_3*(J_3-J_1))):

> z:=sqrt((J_3-J_2)*(L^2-2*E*J_1)/(J_1*J_2*J_3))*t:

> k:=sqrt(((J_2-J_1)*(2*E*J_3-L^2))/((J_3-J_2)*(L^2-2*E*J_1))): K:=EllipticK(k);

> X:=J_1*omega_01*JacobiCN(z,k): Y:=J_2*omega_02*JacobiSN(z,k): Z:=J_3*omega_03*JacobiDN(z,k):

> crv:=plots[spacecurve]([X,Y,Z], t=0..4*K+.25, thickness=3, color=black):

> sph:=plottools[sphere]([0,0,0], L):

> ell:=plottools[scale](sph, sqrt(2*E*J_1)/L, sqrt(2*E*J_2)/L, sqrt(2*E*J_3)/L):

> plots[display]([crv, sph, ell], scaling=constrained);

>

Example 4 . Let us plot the curve of Viviani with the shadow and the revolution about the axis OZ.

In the next program, tube, tube2 denote curves of Viviani (tubes); sphere denotes a sphere (frame);

T denotes a circular tray; shad denotes the parallel projection onto a tray; op(tube) denotes a curve of

Viviani (tube); op(shad(tube2) denotes a shadow of a curve of Viviani (tube).

> restart: with(plots): with(plottools):

Warning, the name changecoords has been redefined

> A:=0: B:=0: C:=1: lv:=55: lh:=70-k*20: oh:=k*20: ov:=75:

> a:=evalf(sin((lv-(90-ov))/180*Pi)*cos((lh+oh)/180*Pi)): b:=evalf(sin((lv-(90-ov))/180*Pi)*sin((lh+oh)/180*Pi)): c:=evalf(cos((lv-(90-ov))/180*Pi)):

> shad:=transform((x,y,z,k)->[((b*B+c*C)*x-a*B*y-a*C*z)/(a*A+b*B+c*C), (-b*A*x+(a*A+c*C)*y-b*C*z)/(a*A+b*B+c*C), (-c*A*x-c*B*y+(a*A+b*B)*z)/(a*A+b*B+c*C)]):

> R:=2: f:=[R*cos(t)^2, R*cos(t)*sin(t), R*sin(t)+R]:

> tube:=tubeplot(f, t=0..2*Pi, radius=.1, color=[.8,.3,.5]): tube2:=tubeplot(f,t=0..2*Pi, radius=.1, color=[.2,.3,.3]):

> T:=plot3d([s,t,0], s=0..2*R, t=0..2*Pi, coords=cylindrical, color=[t/(2*Pi), .7, .2]):

> PLOT3D(ANIMATE(seq([op(T), op(tube), op(shad(tube2)), LIGHT(lv,lh, .8,.3,.5), PROJECTION(oh,ov,.5)], k=1..18)), AMBIENTLIGHT(.5, .5, .5), STYLE(PATCHNOGRID), SCALING(CONSTRAINED));

>

8.4 Trajectories of Vector Fields in Space

1. Three-dimensional vector fields using command fieldplot3d .

> plots[fieldplot3d]([z*y,z*x,x*y], x=-1..1, y=-1..1, z=-1..1, grid=[5,5,5], arrows=SLIM, axes=boxed);

An analogous result is obtained using the command gradplot3d .

> plots[gradplot3d](x*y*z, x=-1..1, y=-1..1, z=-1..1, grid=[5,5,5], arrows=SLIM, axes=framed);

2. The three-dimensional curve (the solution of a system of ODEs) using the command odeplot

> sys:=diff(y(x),x)=z(x), diff(z(x),x)=y(x); p:=dsolve({sys, y(0)=0, z(0)=1}, {y(x),z(x)}, type=numeric): plots[odeplot](p, [x, y(x), z(x)], -4..4, numpoints=25, axes=boxed,thickness=2);

An analogous result (figure) is obtained using the command DEplot3d from the library DEtools .

> DEtools[DEplot3d]({D(x)(t)=y(t), D(y)(t)=-x(t)-y(t)}, [x(t),y(t)],t=0..10, [[x(0)=0,y(0)=1], [x(0)=0, y(0)=.5]], stepsize=.1, tickmarks=[4,3,3]);

3. The command textplot3d allows us to place text in three-dimensional plots.

> plots[textplot3d]([[1,2,3, `First solution`],[2,2,3, `Second solution`]], axes=boxed);

>